

2022年8月20,复旦大学智能复杂体系基础理论与关键技术实验室于玉国教授课题组与华东师范大学陈爱华研究员课题组和神经所顾勇研究员课题组合作,共同在SCIENCE合作期刊Research(IF >11)在线发表了题为“Unveiling Dynamic System Strategies for Multisensory Processing: From Neuronal Fixed-Criterion Integration to Population Bayesian Inference”的研究论文,复旦大学智能复杂体系基础理论与关键技术实验室研究生张佳伟为文章第一作者。
大脑如何对外界环境的多种感觉信息进行综合处理,对于人和动物在自然环境中的生存至关重要。例如,狮子在复杂的森林环境中急速奔跑捕猎麋鹿时,其大脑皮层从各个感官接收运动中的麋鹿图像、穿梭在林木中的声音、以及老虎自身的运动方位、加速度等多种感觉信息,通过整合计算以准确判断自身和目标在环境中的定位以及运动状态。其中的关键步骤是大脑面对不同模态的感觉输入需要推断这些信息是否源自同一物体或事件,从而决定哪些信息应当整合归因为同一来源,哪些应当分离为不同来源。这个过程发生于大脑的什么地方?以什么样的方式进行?遵循什么计算策略?近20年来的实验研究证据表明:皮层多感觉整合加工可能存在一个复杂的前馈和反馈神经环路,可能在某一个特定的感觉皮层就存在多种感觉的整合加工和层级加工,比如已发现猕猴背侧内侧上颞区 (MST-d)可对同时来自视觉信息和前庭本体感觉信息进行整合处理加工。
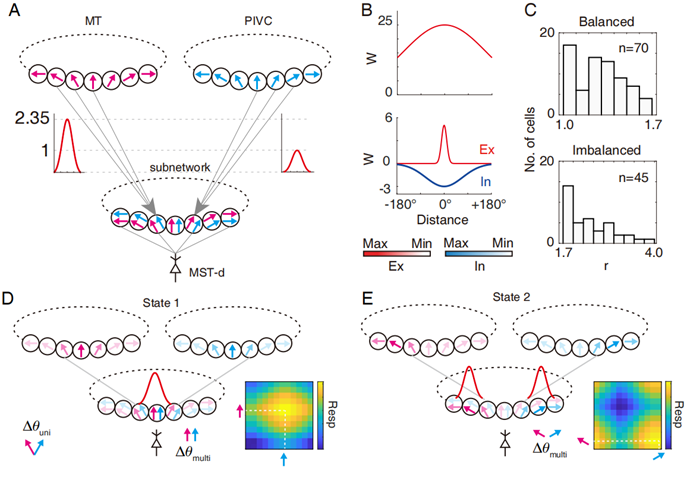
图1.多脑区 CANN 模型结构(A)。B.网络中神经元的前馈输入和侧向耦合的突触连接函数。C.实验数据中来自前庭和视觉的突触强度比例统计分布。D.对于给定的前庭和视觉的多感觉朝向刺激,MST子网络形成一个共同激活区域;插图显示,当接收全等输入时,MST-d 神经元响应达到最大。E. 对于给定的前庭和视觉的多感觉朝向刺激,MST子网络形成一个两个分离的激活区域。插图显示,当接收到几乎相反的输入时,MST-d 神经元响应达到最大。
近年来围绕多感觉信息处理的未解难题主要包括:多感觉脑区处理整合多模态信息的计算机制,在具有各种背景环境噪声的运动过程如何处理信息不确定性,及如何对刺激目标的运动朝向和方位进行概率推断等。在该研究中,陈爱华团队为猕猴设置了视觉与前庭的多感觉刺激条件,深入分析了记录到的脑背侧内侧上颞区 (MST-d) 的神经元电生理数据,于玉国团队构建了跨皮层连续吸引子神经网络 (CANN) 计算模型。通过结合实验数据分析与计算模型机制研究,发现来自前庭和视觉脑区的突触输入强度比例对于MST-d 神经元实施多感觉整合还是分离计算具有决定作用。来自两个上游脑区的突触输入强度比例调控了MST多感觉脑区内部的合作或竞争,并使得单个 MST-d 神经元可应用固定阈值策略在整合与分离的响应之间进行动力学切换。
国际同行之前发表的一系列重要理论模型文章往往把多感知整合和分离现象的计算机制归因于多感觉脑区之间两类神经元的联合计算:congruent (同向)和opposite(反向)神经元。但该项研究指出,congruent (同向)和opposite(反向)神经元不是实现多感觉计算的本质。真正的神经机制在于视觉和前庭两个脑区投射到MST-d多感觉神经元的突触输入强度比例存在差异。当MST-d神经元接收到两类感觉输入强度的比例均衡(接近1)时,其呈现出opposite反向神经元的分离特性;而当两类感觉输入强度比例逐渐失衡(>>1)时,MST-d神经元开始呈现出congruent神经元的整合特性,并且整合特性的权重随比例失衡逐渐升高。总体而言,基于多感觉皮层的突触输入平衡和非平衡比例为多感觉计算提供了更为基础和根本的理论机制。
研究进一步基于上述整合与分离的计算机制构建了蒙特卡洛采样理论模型(fMCS),针对MST神经网络是否执行贝叶斯推断规则进行了严谨的分析。由于突触平衡程度的多样性,MST-d群体神经元具有不同的角度偏好,并在相同的外部刺激条件下表现出不同的激活程度。经过数十万次随机重复模拟计算,fMCS模型对群体的多种激活程度进行采样,解码输入刺激角度隐藏态的后验概率,进而给出整合或分离的决策。fMCS模型良好匹配了传统的贝叶斯策略模型,并验证了大脑多感觉计算的概率推断不需要通过高级认知皮层表征不确定性,而是在单感觉向多感觉脑区的层级信息处理过程中由特定的计算机制直接进行推断。该研究为揭示高等动物多感觉脑区进行多模态信息整合计算和认知推断策略方向提供了基础的生物物理理论机制,对脑启发的人工智能模型进行多模态信息整合计算具有重要启示。
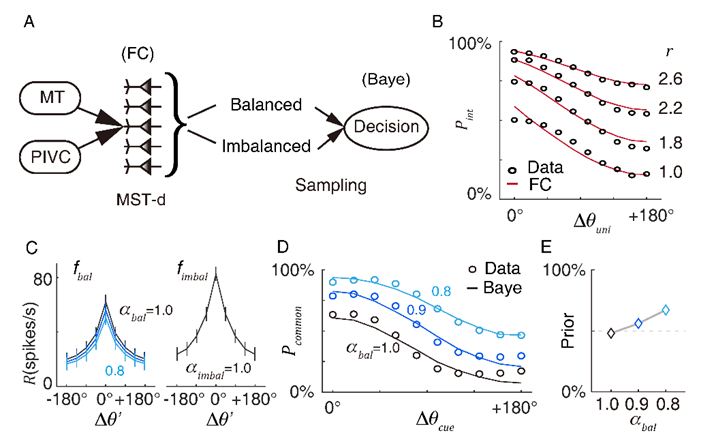
图2.(A)从实施固定标准 (FC) 策略的单个 MST-d 神经元到实施贝叶斯策略的 MST-d 神经元的皮层网络示意图。(B) 具有不同突触比率的神经元整合功能的 FC 策略。(C)平衡和非平衡神经元的多感觉响应函数。(D)从采样过程模拟的决策具有不同突触平衡比例参数值的多感觉整合概率(圆圈)和具有不同先验概率的贝叶斯拟合(曲线)。(E) 贝叶斯函数拟合中的拟合值对调谐函数幅度系数的依赖关系。
Zhang, J., Gu, Y., Chen, A., & Yu, Y. Unveiling Dynamic System Strategies for Multisensory Processing: From Neuronal Fixed-Criterion Integration to Population Bayesian Inference. Research, 2022.











