神经网络为海量数据时代的科学研究提供了强有力的工具。由于神经网络大多是工作在“黑盒”模式下,难以对其原理进行解释从而进一步优化其计算效率。为神经网络的逼近效果或表达能力提供数学理论支持也因此一直以来都是研究人员试图攻克的关键问题。针对多层感知机的万有逼近定理作为深度学习最根本的理论依据,首次对神经网络对任意函数的逼近能力给出了理论刻画。近年来,各类神经网络被广泛提出和发展,其中储备池计算模型作为循环神经网络的一种特殊变体,因其贴近真实生物大脑、计算消耗小、易于物理实现等特征而受到广泛关注,尤其是在对时间演化的动力系统的重构和预测问题中取得了出色的效果。该架构的特点是输入层和储备池层的参数无需训练而随机给定,训练消耗仅存在于对输出层参数的最小二乘拟合。

2023年5月在线发表于Physical Review Research(Volume 5, Article No. L022041)的工作中,复旦大学智能复杂体系基础理论与关键技术实验室林伟教授团队联合苏州大学数学科学学院马欢飞教授团队为储备池计算模型对真实动力系统的逼近能力给出了严格的理论刻画。该工作将储备池内部神经元的状态视作为对真实世界演化的多个不同角度的观测,从而验证了储备池状态更新方程作为外部演化到内部状态的一个嵌入。该理论的发展对储备池计算架构的理论分析进行了完善,进一步,利用Takens嵌入定理所确保的时间延迟和空间分布在观测上的等价性,该工作设计了一种时间信息和空间信息可相互转化的新型储备池计算架构,用现有神经元的过去时间信息来替代对更多数量神经元的需求,从而实现了架构的大幅轻量化。有趣的是,在一定情况下,仅需一个神经元(加上其过去的时间信息)就可以实现相当的重构和预测效果。
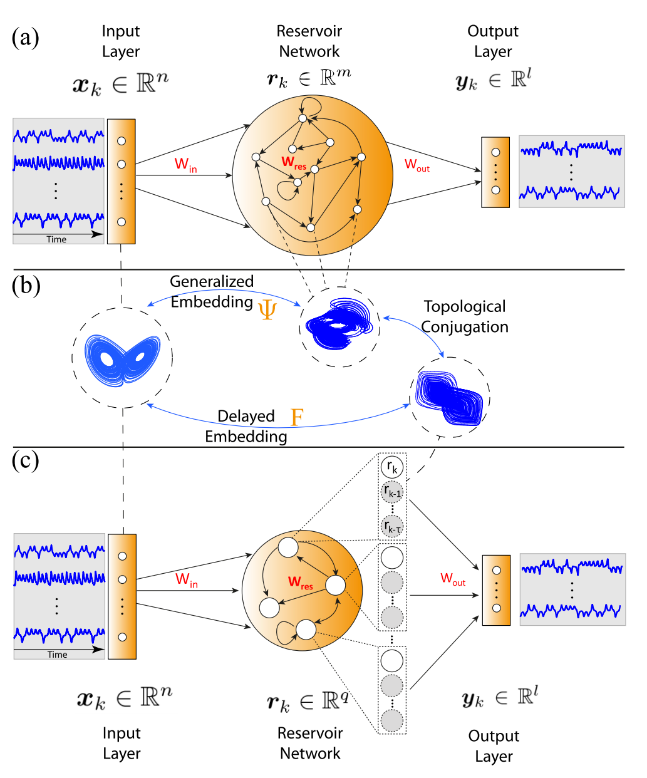
图:基于时空信息互化的轻量级储备池神经网络架构
该计算架构在多个模型和数据集上得到了有效验证,给出了在数学理论的指引下降低神经网络计算消耗的有效途径,也为该神经网络的便捷物理实现提供了帮助。林伟、马欢飞、冷思阳等团队成员多年来致力于应用数学和复杂系统理论的发展,并推动人工智能、数据科学等交叉融合领域中实际应用问题的解决。苏州大学马欢飞教授和林伟教授为本文的共同通讯作者。该研究得到了国家自然科学基金、上海人工智能实验室和上海市市级科技重大专项的资助和支持。
文章链接:https://doi.org/10.1103/PhysRevResearch.5.L022041











