
2024年5月2日,复旦大学林伟教授、朱群喜博士研究团队近期共有3篇论文被国际机器学习顶级学术会议ICML 2024录用,主要涵盖团队在当前主流的生成模型,复杂系统建模,神经控制等方面的最新研究进展,相关论文信息如下。
[生成模型]
论文题目:Switched Flow Matching: Eliminating Singularities via Switching ODEs
作者:朱群喜*,林伟
在OpenAI发布Sora[1]后不久,Stability AI推出了Stable Diffusion 3(SD3)的技术报告[2]。与Sora不同,SD3采用了一类连续时间的生成模型,取得了显著的效果。连续时间的生成模型,如Flow Matching(FM)[3],通过学习神经常微分方程(NODEs)[4]来构建概率路径,通过无模拟的训练方式实现一个分布和另一个分布之间的变换。
然而,在推断过程中,训练后的模型通常需要多次数值迭代才能到高质量的样本,导致采样速度较慢。在本工作中,我们将这个原因归因于源分布和/或目标分布的固有(联合)异质性,即奇异性问题,这给训练NODEs带来了巨大挑战。为此,我们首先从理论上指出了FM的缺陷,并提出了一个更一般的框架,称为Switched FM(SFM),通过切换ODEs来消除FM框架面临的奇异性。此外,我们的框架可以与现有理论技术进行无缝融合,如最优输运理论,以进一步提高概率流的平直程度,从而实现更高效的采样过程并降低成本。

图1:(奇异)最优传输映射(a),(更好)近似最优传输映射(b, c)。
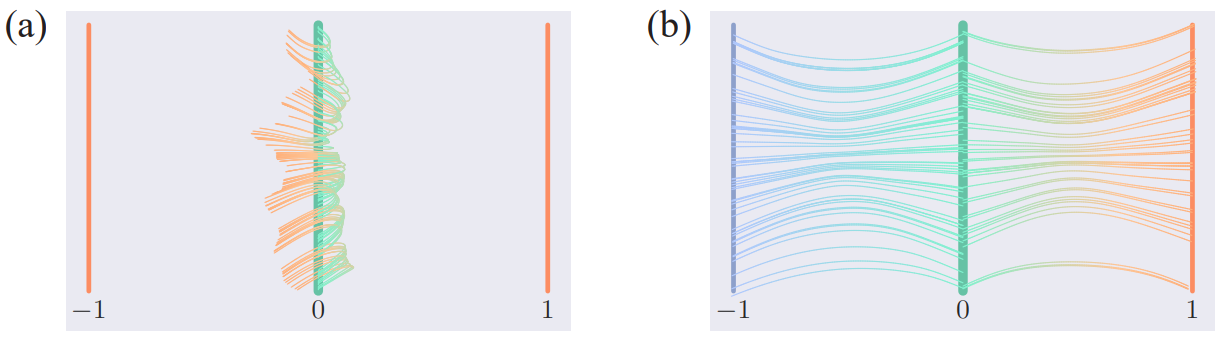
图2:FM和SFM学到的流(a)和(b)。
图1展示了将中间棍子搬运到两侧棍子面临的最优传输映射的奇异性问题,存在无穷多个奇异点,并且可以通过有限个奇异点的传输映射来近似最优传输映射。图2则展示了训练后FM和SFM的流,可以看到FM完全无法实现传输。此外,我们还在文中展示了多个数值示例验证提出的SFM的有效性。
[复杂系统建模]
论文题目:From Fourier to Neural ODEs: Flow Matching for Modeling Complex Systems
作者:李鑫,张静东,朱群喜*,赵城利*,张雪,段晓君,林伟
在现代科学研究中,连续复杂系统的建模受到广泛关注,通常依赖于神经常微分方程(Neural ODEs, NODEs)[4]。然而,这种方法在应用过程中面临着高计算成本和易陷入局部最优的问题。为了应对这些挑战,我们提出了一种新的无模型框架——傅立叶神经微分方程(Fourier Neural ODEs, FNODEs),通过傅立叶变换直接匹配目标向量场来有效训练神经网络的参数。
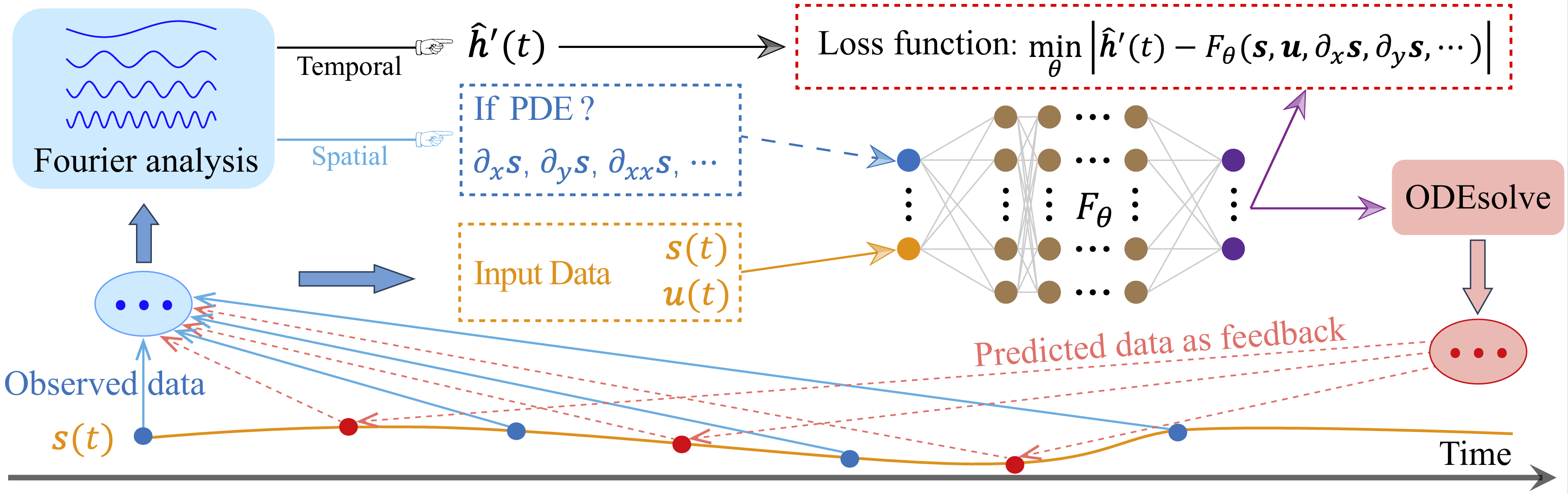
图3:傅里叶神经微分方程框架的示意图
图3展示了我们方法的执行过程。具体而言,我们利用傅立叶分析从含噪声的观测数据中估计时间梯度和所有潜在的空间梯度,并将观测数据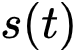 ,变化的参数
,变化的参数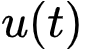 ,以及所有估计的空间梯度
,以及所有估计的空间梯度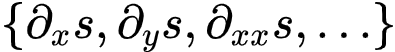 作为神经网络的输入。同时,我们使用估计的时间梯度作为神经网络输出的优化目标,从而实现更高效且鲁棒的建模。此外,经过训练的NODEs可以通过常微分方程求解器生成更多数据点,这些新增的数据点可以促进傅立叶分析更精确的估计梯度。因此,傅里叶分析和神经微分方程技术互为补充,能分别从谱分析和微分动力学的视角对观测数据进行处理,从而使得我们的框架能够在动力学建模任务中实现更优的表现。
作为神经网络的输入。同时,我们使用估计的时间梯度作为神经网络输出的优化目标,从而实现更高效且鲁棒的建模。此外,经过训练的NODEs可以通过常微分方程求解器生成更多数据点,这些新增的数据点可以促进傅立叶分析更精确的估计梯度。因此,傅里叶分析和神经微分方程技术互为补充,能分别从谱分析和微分动力学的视角对观测数据进行处理,从而使得我们的框架能够在动力学建模任务中实现更优的表现。
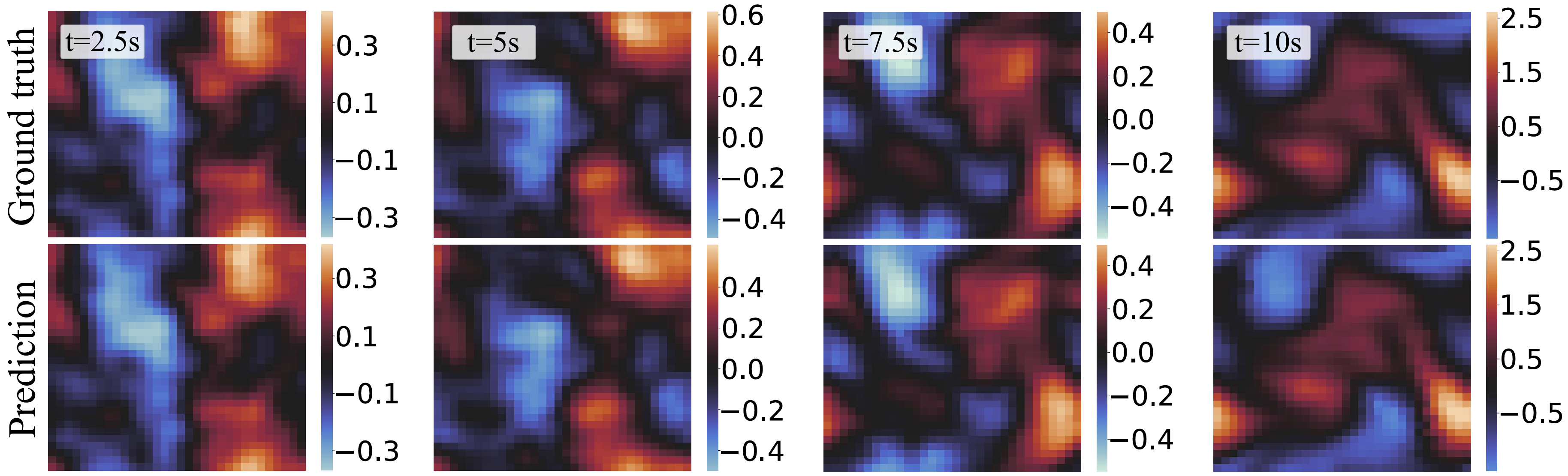
图4:使用FNODEs方法建模并预测2维Navier-Stokes系统。
通过对几种代表性复杂系统的测试,我们的方法在训练时间、动力学预测和鲁棒性方面均相较于基线方法表现出更好的性能。特别是在偏微分方程系统的建模任务中,我们的方法不仅实现了分辨率不变的建模,还充分利用了潜在的空间偏导项这一物理先验,从而可以通过神经网络高效的建模偏微分方程的复杂非线性动力学,实现更加精确的动力学预测(图4展示了我们的方法在Navier-Stokes系统中的预测表现)。
[神经控制]
论文题目:FESSNC: Fast Exponentially Stable and Safe Neural Controller
作者:张静东,杨鸾,朱群喜*,林伟*
自然、科学和工程界中的许多实际问题可以建模为包含噪声的随机动力系统,由于动力系统的主要信息蕴含在系统平衡态内,如何设计合适的控制器将随机系统镇定到不稳定平衡态,成为相关领域的热门研究问题。先前的工作集中在为控制器的稳定性或者受控系统的安全性提供数值保证,如何设计理论上同时具有稳定性和安全性保证的控制器是该领域亟待解决的问题。为攻克这一难题,本团队前期结合数学理论和机器学习,建立了基于安全性保证的神经随机控制理论与方法[5, 6]。本工作进一步提出了神经网络控制器的伪投影方法,将用神经网络学习到的镇定控制器投影到稳定且安全的控制函数空间。
具体地,针对稳定性保证,研究者首先基于随机动力系统的指数稳定性理论设计了求解镇定控制的优化问题,再利用拉格朗日乘子法将硬性约束加到目标函数中转化为软约束,并用神经网络来求解这一问题。在得到神经网络镇定器后,研究者通过将其投影到严格满足稳定性条件的控制函数空间来为其提供稳定性保证,由于该投影算子缺乏解析表示,研究者设计了具有解析表达的伪投影算子来近似投影算子(图5)。由于该算子是投影算子在控制函数空间中的近似,因此仍然能够保证伪投影后的镇定器落在目标空间内。类似对于安全性保证,研究者基于零障碍函数理论,提出了相应的优化问题和伪投影算子。进一步,研究者证明了同时具有稳定性和安全性的控制函数空间的存在性。最后,通过稳定性伪投影算子和安全性伪投影算子的复合作用,研究者得到了具有稳定性和安全性保证的镇定器。
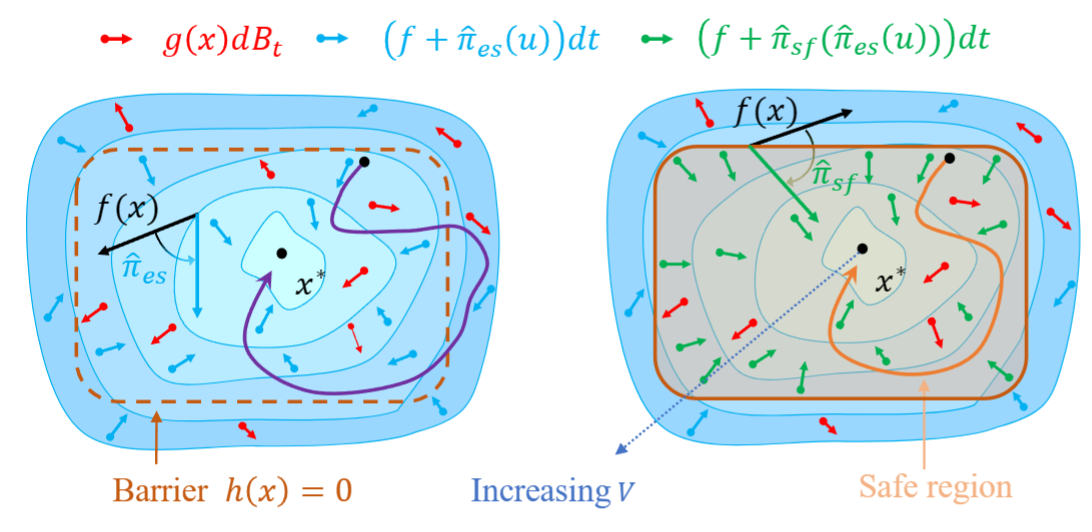
图5: 伪投影算子示意图。受控向量场(蓝、绿箭头)落在稳定性和安全性的区域内。
为提升神经网络控制器在不同尺度模型中的训练效率,研究者基于矩阵求迹算子的性质,为损失函数中的高阶项设计了基于高斯噪声的无偏估计,将模型的计算复杂度从二次阶降到了线性阶。该方法在几种代表性控制问题的测试中均取得最佳表现,表1展示了不同方法在双臂倒立摆镇定任务中的表现,本文方法FESSNC不仅在训练时间和成功率上远超近几年的其他方法,研究者还发现其在控制过程中的能量消耗(Control energy)最低,造成这一现象的原因有待未来进一步探索。
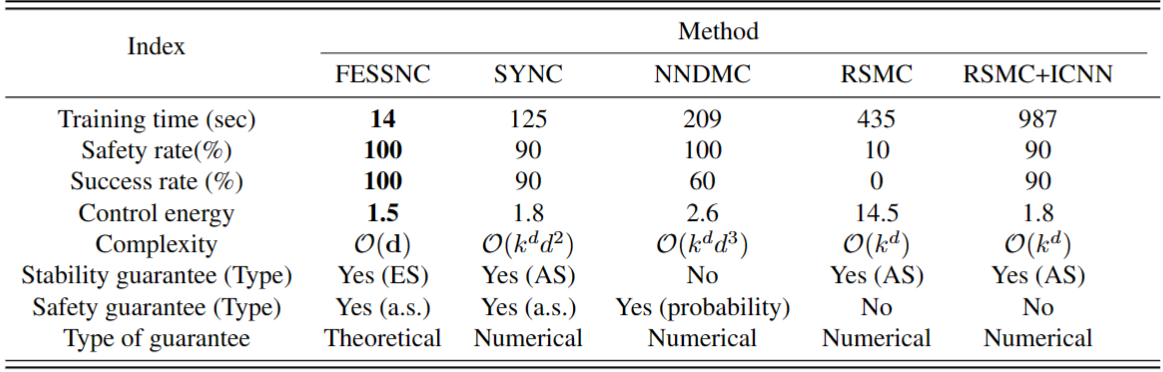
表1: 不同机器学习镇定控制方法的性能比较。
复旦大学智能复杂体系基础理论与关键技术实验室林伟教授对以上研究提供了重要的指导和建议,合作团队有国防科技大学赵城利副教授课题组。研究得到了中国博士后科学基金、上海市超级博士后计划、上海市启明星杨帆专项计划以及上海市科学技术委员会、国家自然科学基金委、上海人工智能实验室、CFFF计算平台的支持。
ICML是机器学习领域的顶级学术会议,全称为国际机器学习会议(International Conference on Machine Learning)。作为机器学习领域的国际顶级会议(CCF-A类),ICML每年举办一次。该会议由国际机器学习协会(International Machine Learning Society)主办。ICML 2024投稿9,473篇,接受2,609篇,录用率为27.5%,会议将于7月份在奥地利的维也纳举行。
【参考文献】
[1]. OpenAI. https://openai.com/index/sora/
[2]. Esser P, Kulal S, Blattmann A, et al. Scaling rectified flow transformers for high-resolution image synthesis. arXiv preprint arXiv:2403.03206, 2024.
[3]. Lipman Y, Chen R T Q, Ben-Hamu H, et al. Flow matching for generative modeling. International Conference on Learning Representations (ICLR) 2023.
[4]. Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations. Advances in Neural Information Processing Systems (NeurIPS), 2018.
[5]. Zhang J, Zhu Q, Yang W, Lin W. SYNC: Safety-aware neural control for stabilizing stochastic delay-differential equations. International Conference on Learning Representations (ICLR), 2023.
[6]. Zhang J, Zhu Q, Lin W. Neural stochastic control. Advances in Neural Information Processing Systems (NeurIPS), 2022.
[7]. Zhu, Q, Lin. Switched Flow Matching: Eliminating Singularities via Switching ODEs, International Conference on Machine Learning (ICML), accepted, May 2, 2024.
[8]. Li X, Zhang J, Zhu, Q, Zhao C, Zhang X, Duan X, Lin W. From Fourier to Neural ODEs: Flow Matching for Modeling Complex Systems. International Conference on Machine Learning (ICML), accepted, May 2, 2024.
[9]. Zhang J, Yang L, Zhu, Q, Lin W. FESSNC: Fast Exponentially Stable and Safe Neural Controller, International Conference on Machine Learning (ICML), accepted, May 2, 2024.











