In recent years, biorhythm has been proven to be intricately linked to human health and has garnered increasing attention from researchers. Notably, in 2017, the Nobel Prize in Physiology or Medicine was awarded for groundbreaking work on biorhythm [1]. Apart from the well-known circadian rhythm (with a cycle of approximately 24 hours), other rhythmic regular changes exhibited within the body can collectively be referred to as biological rhythms. These include neuronal action potentials, gene-protein transcription translation processes, and vital heartbeat functions. As two crucial physical quantities, the frequency and amplitude of biorhythm respectively determine the characteristics and intensity of upstream signals while also influencing downstream activities [2].
Consequently, any abnormal frequency or amplitude caused by various factors can lead to rhythm disorders and subsequently result in physiological ailments such as sleep disorders and type 2 diabetes [3]. Therefore, precise regulation of the frequency and amplitude of biological rhythms to restore them to normalcy has become an important scientific challenge. Initially, some scholars conducted pioneering studies on the relationship between frequency-amplitude tunability and feedback loop modes within rhythmic systems through extensive calculations [4]. More recently, certain scholars have proposed biologically feasible frequency-amplitude controllers that have also been validated through calculations [5]. However, there is still a lack of systematic universal theoretical progress concerning regulating the frequency and amplitude of biorhythms. Moreover, there remains a dearth of mathematical theoretical calculation methods for advanced controller design capable of accurately adjusting frequency amplitudes within complex space-time systems.
In response to these issues, on October 8, 2021, Dr. Qin Bowei, Dr. Zhao Lei, and Professor Lin Wei from Fudan Mathematics published a research article titled ' A frequency-amplitude coordinator and its optimal energy consumption for biological oscillators' in Nature Communications online. The article presents a frequency-amplitude coordinator and its optimal energy consumption for biological oscillators. The controller is meticulously designed using rigorous mathematical theory and a universal calculation method to precisely adjust the intrinsic frequency and amplitude of spatiotemporal biological oscillators. This methodology can be applied to biorhythm models with diffusivity at various scales while enabling control over their frequency and amplitude. These findings also extend earlier theoretical results [6] on frequency-amplitude modulation of biological oscillatory systems into the realm of 'spatiotemporal complex systems.'
The researchers employed Michaelis-Menten regulation to modulate protein expression levels within an abstract spatio-temporal model of gene regulatory networks. In this model, once the protein concentration surpasses a certain threshold, it enters the 'cancer zone.' Through carefully designed controllers, gradual reduction of protein concentration back to normal levels can be achieved (Figure 1).
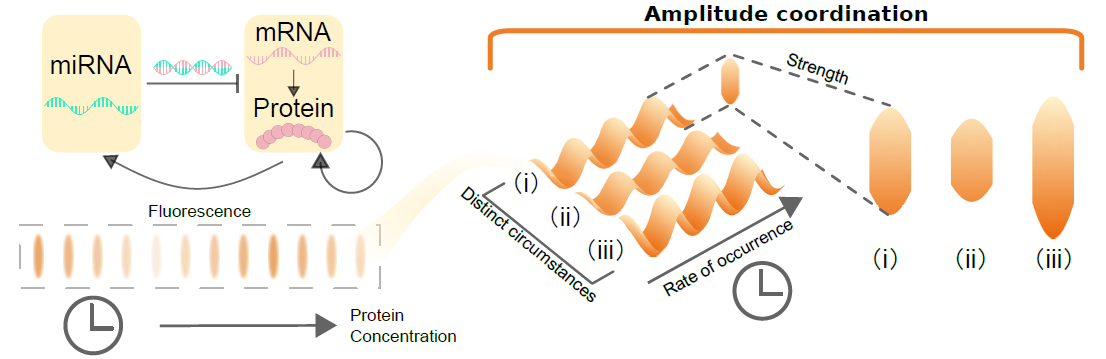
Fig 1: Amplitude coordination in abstract spatiotemporal model of gene-protein interaction
The researchers then utilized dynamical system theory to elucidate the effective adjustment of frequency and amplitude through this control method, providing a detailed calculation methodology. For oscillations resulting from bifurcation, perturbation is applied to the intrinsic linear action of the biological oscillator using the linear region of the Mi function, leading to significant changes in both frequency and amplitude. By employing rigorous calculations involving central manifold and normal-type theory (Figure 2), the relationship between perturbation intensity and variations in frequency amplitude can be unveiled.
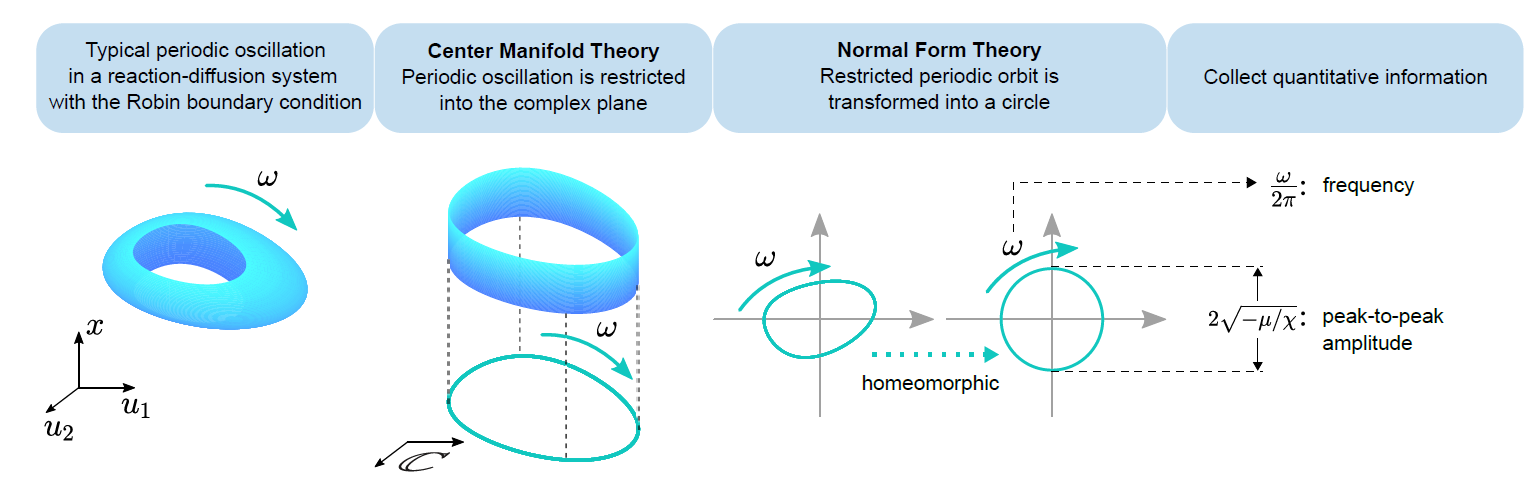
Fig 2: The frequency and amplitude information is extracted through the application of dynamic theory
Using these methods, the researchers successfully achieved frequency modulation of the spatio-temporal neuron model (FitzHugh-Nagumo), thereby confirming the method's universality (Figure 3). Furthermore, it was revealed that the controller follows a general law where the frequency-amplitude regulator acts as a disturbance to the intrinsic linear action. This disturbance can only enhance or weaken the intrinsic action simultaneously (Figure 4). Consequently, the designed controller can be considered as an amplifier or a damper. Lastly, considering energy consumption, the researchers were able to select an optimal controller based on this criterion.
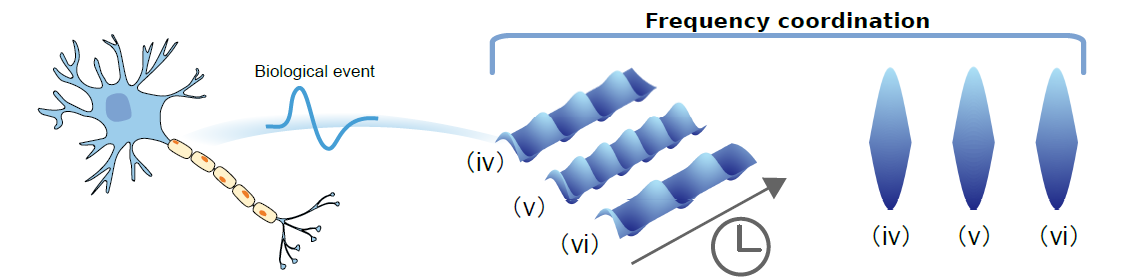
Fig 3: Amplitude coordination in neuron model
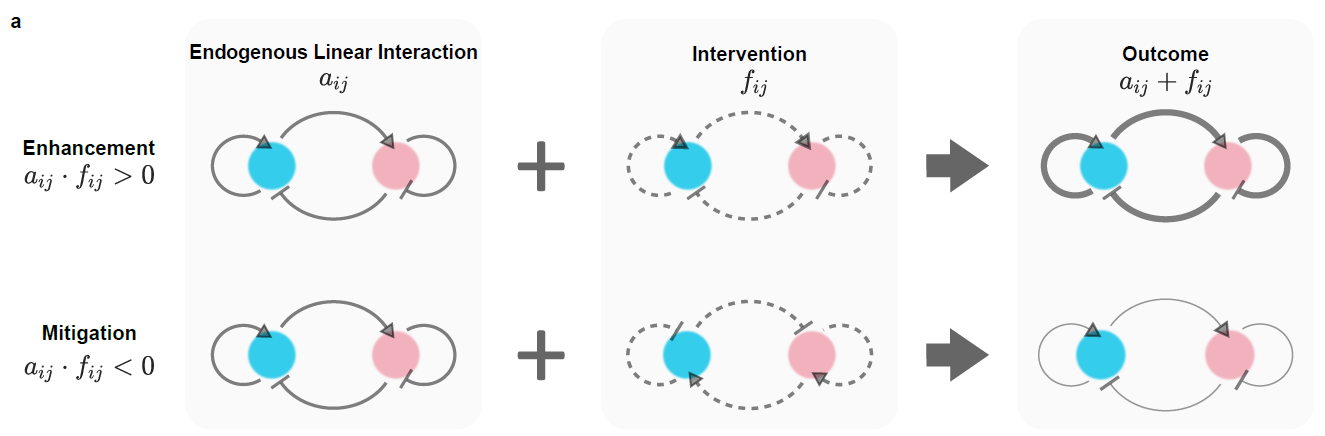
Fig 4: the general rules of the controller designed by the institute
In this study, the researchers integrated biological science problems with applied mathematical methods closely and proposed a viable regulatory approach. This approach can offer theoretical support for experimental research on biological rhythms FM and AM, thereby potentially accelerating future advancements in this field. Dr. Qin Bowei, a postdoctoral fellow in mathematics at Fudan University, is the primary author of this work, while Dr. Qin Bowei and Professor Lin Wei are co-corresponding authors. Funding for this research was provided by the National Natural Science Foundation of China, the Frontier Center of Brain Science of the Ministry of Education, the Key Research Project of the Ministry of Science and Technology, the Shanghai Municipal Major Project, the China Postdoctoral Foundation, as well as by the Key Laboratory of Nonlinear Mathematical Models and Methods and Key Laboratory of Computational Neuroscience and Brain-like Intelligence under the Ministry of Education.
Paper Link:https://www.nature.com/articles/s41467-021-26182-2
Reference:
Callaway, E. & Ledford, H. Medicine Nobel awarded for work on circadian clocks. Nature550, 18 (2017).
Hansan, A. S. & O’Shea, E. K. Limits on information transduction through amplitude and frequency regulation of transcription factor activity. eLife4, e06559 (2015).
Bass, J. & Takahashi, J. S. Circadian integration of metabolism and energetics. Science330, 1349-1354 (2010).
Tsai, T. Y.-C. et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science321, 126-129 (2008).
Tomazou, M.et al. Computational re-design of synthetic genetic oscillators for independent amplitude and frequency modulation. Cell Systspans6, 508-520.e5 (2018).
Ge, T. et al. Achieving modulated oscillations by feedback control. Physical Review E90, 022909 (2014).











