Many real-world problems can be represented as dynamic systems, and the equilibrium state of these systems contains crucial information. The stabilization of dynamic systems with unstable equilibrium states is highly significant in the field of control [1]. Due to the influence of random noise and response delay, it is necessary to incorporate random terms and delay terms into the corresponding dynamic system for modeling purposes [2]. However, there is currently a lack of theoretical research on safety stabilization issues concerning stochastic dynamical systems with time delay, as well as algorithm design for stabilizers.
On January 15, 2023, Lin Wei's team from Fudan University's Research Institute of Intelligent Complex Systems published a paper titled SYNC: Safety-Aware Neural Control For Stabilizing Stochastic Delay-Differential Equation in International Conference of Learning Representation (ICLR)[3]. In this paper, the researchers proposed theories regarding stability and safety in stochastic time-delay dynamical systems. By utilizing neural networks and barrier function methods, they pioneered the construction of stabilizers for stochastic time-delay dynamical systems that ensure both stability and safety. This includes both deterministic stabilizers and stochastic stabilizers. Furthermore, they established theoretical estimates for energy loss in these stabilizers as well as upper bounds for stabilization time. The discovery that stochastic control outperforms deterministic control in certain situations provides valuable insights into understanding and harnessing the effects of noise.

1. A neural network-based deterministic stabilizer relying on LaSalle-type theorem
Firstly, the researchers derived sufficient conditions for the LaSalle-type principle [4], which characterizes the stability of stochastic dynamical systems with time delay. They then obtained a loss function that is conducive to training neural networks effectively. Next, they employed regularization methods to construct parametric neural networks and successfully obtained the deterministic stabilizer (NDC) of neural networks based on the LaSalle principle. These stabilizers can be easily implemented in both autonomous and non-autonomous stochastic time-delay dynamical systems. Figure 1 illustrates the application of NDC in Chua's circuit driver-corresponding system. In comparison with the traditional linear feedback stabilization method (LC) based on global Lyapunov functions [5], NDC exhibits superior performance in both autonomous (Figure 1(c)) and non-autonomous (Figure 1(d)) scenarios. However, due to the presence of an Ito differential operator in the LaSalle principle, which introduces dissipative terms into a positive form within the loss function, this approach cannot be utilized for identifying random stabilizers. Consequently, researchers have proposed a novel stability theory aimed at discovering random stabilizers.
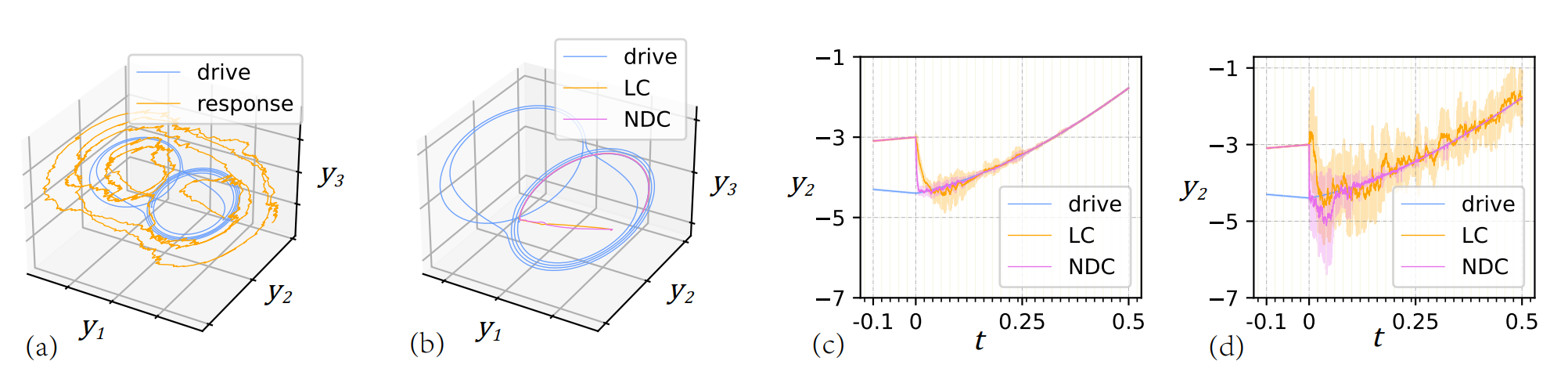
Fig 1: Application of deterministic stabilizer in drive-response system.
(图源:J Zhang, et al., ICLR, 2023)
2. Stochastic stabilizer based on neural network
Based on the second-order differential properties of fractional state variables, we establish the stability theory of stochastic functional systems with simple conditions (stochastic delay systems are special stochastic functional systems). Subsequently, we construct the neural network stochastic stabilizer (NSC). This method can be utilized to identify both random and deterministic stabilizers. FIG. 2 illustrates the results obtained from implementing the constructed stabilizer in controlling a moving vehicle to reach its target position. In comparison to quadratic programming (QP) based on online learning, NDC and NSC can provide instantaneous control values based on current observation states, making them more suitable for real-time control tasks. When compared to NDC, NSC exhibits greater fluctuations in orbit but also achieves faster attainment of the target position.
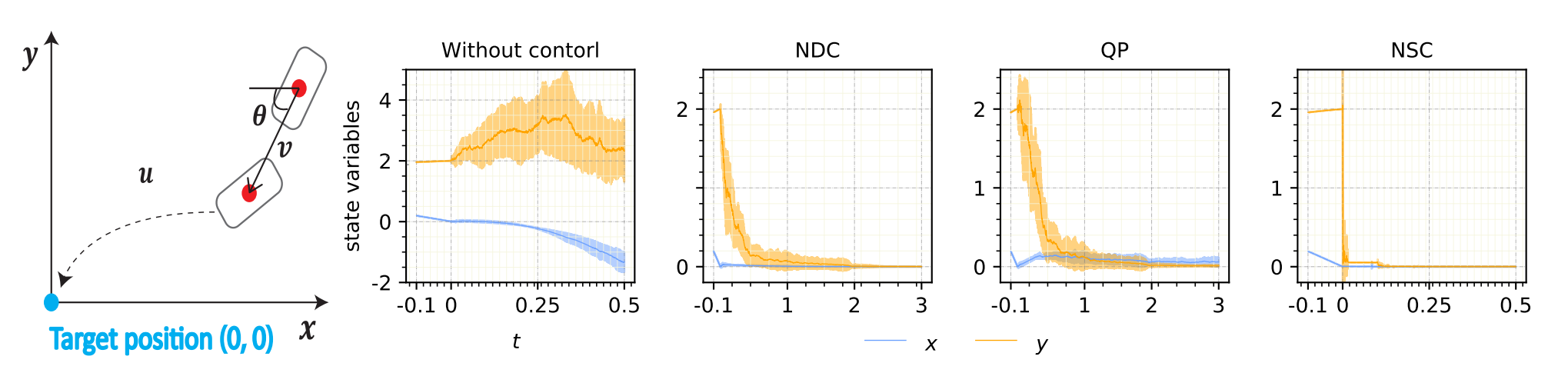
Fig 2: Application of stochastic and deterministic stabilizers in kinematic bicycle model
(图源:J Zhang, et al., ICLR, 2023)
Furthermore, we calculate and analyze the performance of different stabilators in a vehicle motion task. Herein, Tt represents the time required for training the neural network; E0.001 denotes energy consumed by the control process before time Tt; Nd signifies shortest distance from controlled track to target position; and E indicates when mode length of controlled track first reaches 0.001. By comparing these calculated indices, our research reveals that random stabilizers necessitate minimal time and energy consumption. This finding suggests that randomness is not detrimental to system stability but rather contributes positively under appropriate design conditions. To validate this discovery further, theoretical estimates regarding convergence time and energy consumption for both stochastic and deterministic stabilizers are established.

Table 1: Results on kinematic bicycle model
(表源:J Zhang, et al., ICLR, 2023)
3. Security and stability assurance of neural network-based stabilizer
Unlike deterministic dynamical systems, a notable characteristic of stochastic dynamical systems is the unboundedness of phase space orbits for stable dynamical systems. In other words, there is no guarantee that system orbits will remain within the specified safe zone (FIG. 3 left). Additionally, due to finite data processing capabilities of computers, the neural network stabilizer based on heuristic learning cannot ensure stability conditions for the controlled system across the entire space. To address these issues, researchers initially proposed a safety theory for stochastic time-delay dynamical systems based on obstacle function theory [6], which achieved safety in terms of probability 1. Building upon this security theory and employing local Lipschitz conditions and finite partitioning on bounded regions (FIG. 3 right), researchers discretized the security region into finite grids and established strong security conditions at grid points. By satisfying these strong security conditions at grid points using them as training samples and loss functions respectively, the neural network stabilizer's security can be guaranteed. Once assurance of system security is obtained, the solution existence space becomes the safe region. Similar to ensuring security guarantees, stability of the neural network stabilizer can be ensured by conducting similar discretization operations within this region.FIG. 4 demonstrates how a safety-assured neural network stochastic stabilizer performs in stabilizing unstable inverted pendulum tasks compared to online optimization methods (QP, MPC) and original stochastic stabilizers; it effectively satisfies imposed security constraints.

Fig 3: Stable stochastic systems do not necessarily satisfy the safety constraint (left). Discretization operation (right).
(图源:J Zhang, et al.,ICLR, 2023)
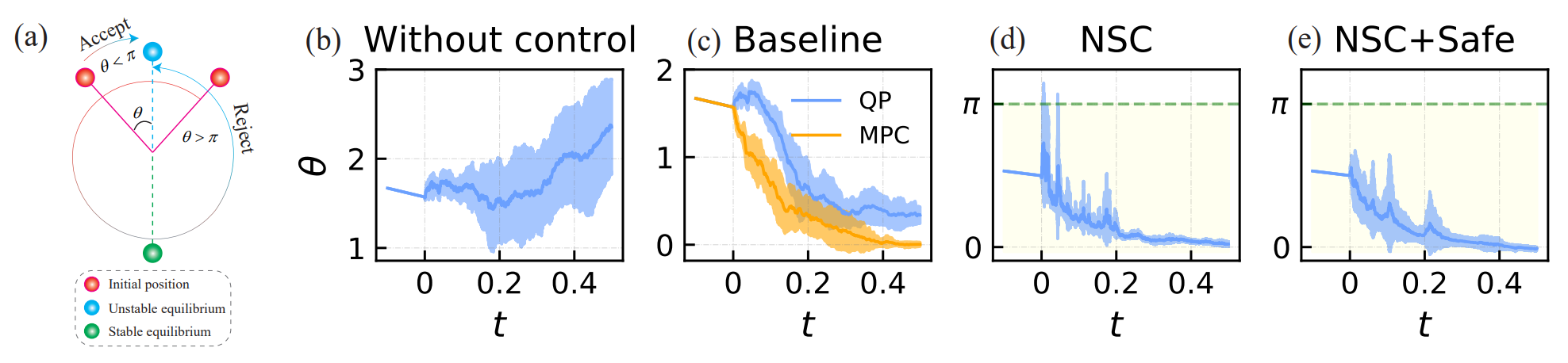
Fig 4: Performance of safety-assured random stabilizer in inverted pendulum task
(图源:J Zhang, et al., ICLR, 2023)
To summarize, this research is the first worldwide to establish the theory of stability and security in stochastic control for stabilizing stochastic dynamic systems with time delay. Additionally, it introduces a neural network stabilizer algorithm to ensure stability and security. Based on experimental data, the performance of deterministic and stochastic stabilizers is calculated and analyzed in terms of energy consumption and controlled orbit convergence time. Compared to deterministic control, stochastic control exhibits lower energy consumption and faster convergence time. This study provides novel insights into the role of noise in complex systems, highlighting its potential utilization through appropriate design rather than suppression as an inconvenience. However, it should be noted that there are still some limitations in the current study. For instance, it primarily relies on model-based approaches and cannot be directly applied to model-free scenarios based on data. Furthermore, considering that the system under investigation has a low degree of freedom at present, future theoretical research is required for stabilization control in high-degree-of-freedom systems.
Paper Link:
This researcher focuses on neural network controllers, and this paper is part of a series of research findings [7]. Dr. Jingdong Zhang from Fudan University serves as the primary author, while Zhu Qunxi, a postdoctoral fellow at the Intelligent Complex Systems Laboratory of Fudan University, Senior Engineer Yang Wei, and Professor Lin Wei are co-corresponding authors. The research received support from various sources including the China Postdoctoral Science Foundation (2022M720817), Shanghai Super Postdoc Program (2021091), Shanghai Science and Technology Commission (22JC1402500, 22JC1401402, 2021SHZDZX0103, 21511100200, 22ZR1407300), as well as the National Natural Science Foundation of China (11925103).
Reference:
[1] Wiener, N.(2019).Cybernetics Or Control And Communication In The Animal And The Machine. MIT Press. Cambridge.
[2]Xuerong Mao.(2007).Stochastic Differential Equations And Applications. Woodhead Publishing. Cambridge.
[3] Zhang, J., Zhu, Q., Yang, W., & Lin, W. (2023). SYNC: Safety-aware neural control for stabilizing stochastic delay-differential equations. In The Eleventh International Conference on Learning Representations.
[4] Xuerong Mao. Lasalle-type theorems for stochastic differential delay equations. Journal of mathematical analysis and applications, 236(2):3.
[5] Wei Lin and Yangbo He. Complete synchronization of the noise-perturbed chua’s circuits. Chaos:
An Interdisciplinary Journal of Nonlinear Science, 15(2):023705, 2005.
[6] Ames, A. D., Xu, X., Grizzle, J. W., & Tabuada, P. (2016). Control barrier function based quadratic programs for safety critical systems. IEEE Transactions on Automatic Control, 62(8), 3861-3876.
[7] Zhang, J., Zhu, Q., & Lin, W. Neural Stochastic Control. In Advances in Neural Information Processing Systems.











