2024年2月20日,复旦大学智能复杂体系实验室团队在 Physical Review Research 以 Letter 形式发表题为“Learning Hamiltonian neural Koopman operator and simultaneously sustaining and discovering conservation laws”的研究文章[1]。该工作中,研究人员构建了数理先验信息嵌入式机器学习框架,实现了从噪声污染数据和部分观测数据中重构哈密顿系统的目标,该框架能够自动保持并发现物理系统的守恒定律,并在不同尺度的任务中均取得最佳表现(state-of-the-art, SOTA)。国际知名学术网站Phys.org以“A machine learning predictor enhances capability for solving intricate physical problems”为题专文推送了该工作的介绍。

从观测数据中发现内在的物理规律是人类长期以来认识世界的方式,如哥白尼提出日心说[2], 开普勒以椭圆轨道修正日心说中的圆轨道[3]。然而,从繁杂的数据中提取模型的动力学或是发现物理规律往往要花费科学家大量的时间以及需要极强的专业知识。近年来,随着人工智能领域的蓬勃发展,如何利用人工智能从噪声或部分观测数据中精准重构底层物理系统,进而辅助科学家发现新的物理规律成为前沿领域的研究热点[4]。当前主流的研究方式是根据物理先验信息,设计启发式神经网络框架,将希望满足的物理规律通过损失函数等“软约束”的方式赋予模型[5];或者加强物理先验信息以实现对模型的结构拆解,进而设计神经网络框架进行分块式学习[6]。尽管这些方法在特定的任务中取得了显著的成果,但由于其缺少对物理规律的“硬约束”,即严格保证模型满足特定物理规律,或对物理先验信息的要求很多,往往很难作为通用性方法被应用到不同尺度的物理系统中。
基于此背景,为实现从噪声污染或者观测不全的数据中精准重构底层物理系统,并挖掘其背后的物理规律,研究者在本工作中构建了数理信息嵌入式机器学习框架(HNKO),通过结合哈密顿系统的库普曼算子理论、酉算子上的李代数理论和黎曼流形上的自编码器技术,HNKO能够实现自动保持物理系统的守恒律、自动识别噪声与真实数据并且包含了哈密顿系统大量的守恒律(图1)。通过对自编码器隐空间的库普曼酉算子进行谱分析,研究者进一步提取出了哈密顿系统的守恒律。研究者首先在经典三体问题中验证了HNKO的有效性,实现结果表明本研究所提出的框架超过了目前该领域所有主流的方法,并且能够从噪声污染数据中提取守恒律(图2)。
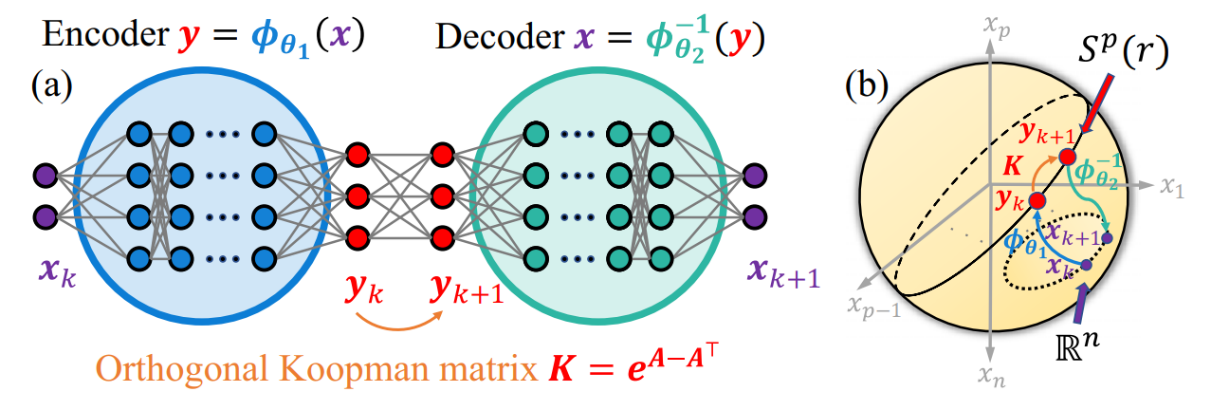
图1 HNKO框架示意图. (a) 基于库普曼酉算子的自编码器. (b) 自编码器是n维欧式空间中的观测数据流形到高维球面上的隐流形的同胚.
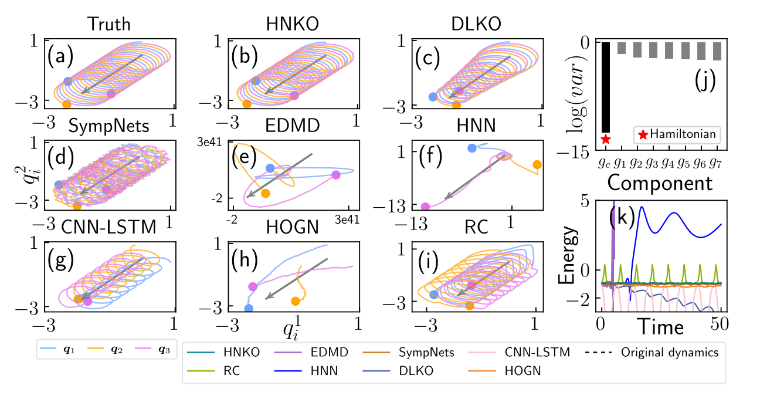
图2三体问题实验结果. (a-i) 本研究所提出框架HNKO与主流方法在三体问题重构、预测中的表现. (j) 对HNKO进行谱分析得到守恒律. (k) HNKO自动保持能量守恒.
接着,针对刚性系统在噪声扰动下难以区分扰动与真实数据这一问题,进一步测试了HNKO在自动识别噪声方面的性能,得到了实验结果的有力支撑(图3)。为进一步解释本框架在自动识别噪声方面的优越性,研究者提出一个新的刚性指标STI,理论论证了本框架能够自动保持STI,而前述方法所提出的刚性指标SAI无法被自动保持[7]。
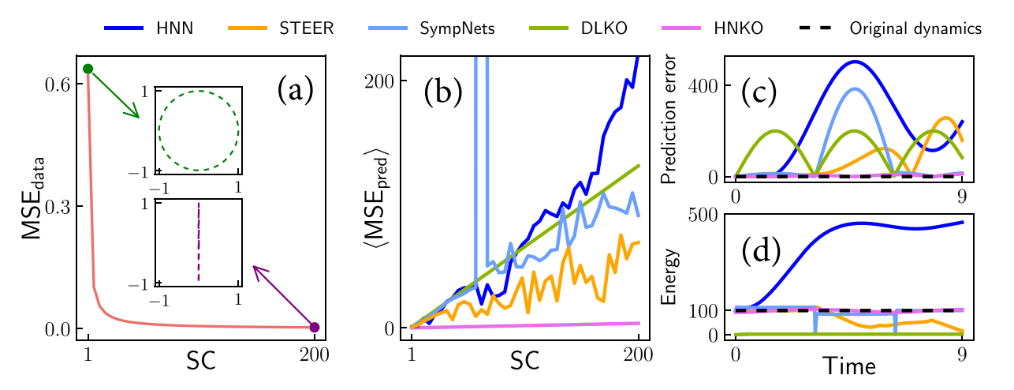
图3 刚性系统实验结果. (a) 不同刚性系数(SC)下的信噪比. (b) 不同SC下重构模型预测轨道的误差. (c-d) 预测轨道误差和能量随着时间的变化.
进一步,对于长期以来广受关注的三维空间n体问题,研究者在拉奎拉大学Fusco研究组关于24体问题代数解方法[8](Inventiones Mathematicae, 2011)的基础上,验证了HNKO在完全或部分观测数据下重构系统并预测周期轨道的有效性(表1)。最后,研究者提出利用克罗内克积对自编码器进行适当分解,降低模型计算复杂度,通过这一技术可将HNKO更高效地应用于高维系统,研究者在水波方程这一流体问题中验证了该技术的有效性(表2)。
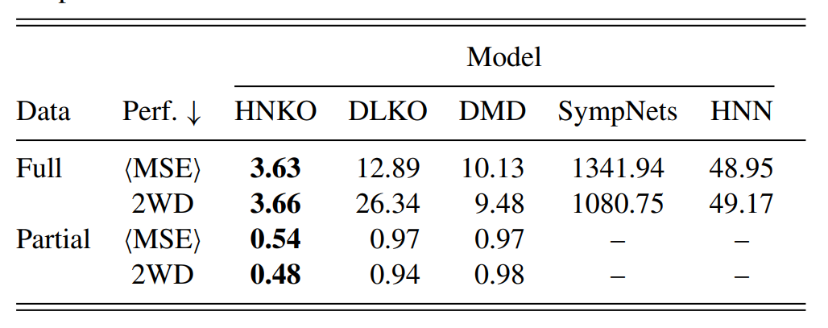
表1不同方法在全观测数据(Full)和部分观察数据(Partial)下的24体周期轨道预测结果,包括预测状态误差和轨道形状误差2WD.
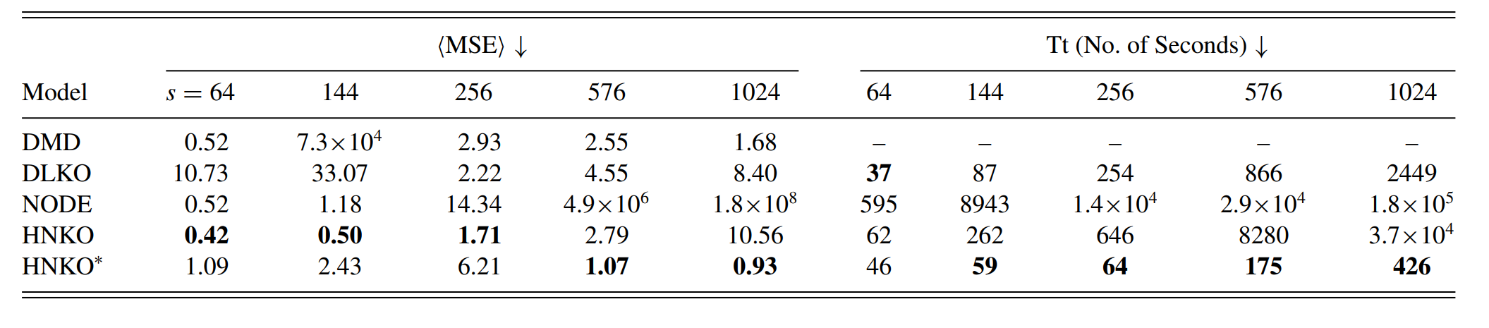
表2不同方法在水波方程例子中实验结果. 表示引入克罗内克积分解的HNKO方法,表格展示了各方法在不同维数的任务中的预测误差和训练所需的时间(Tt).
综上所述,该研究将数理先验信息嵌入到了神经网络框架的结构当中,与当前主流的物理启发式神经网络(PINN) [9]相比,该框架建模的系统能够实现关于物理规律的“硬约束”而非“软约束”,这一关键特征保证了该框架在不同场景中的鲁棒性和灵活性。该框架在引力系统、刚性方程和流体问题等不同时空尺度的任务中均取得SOTA效果,且模型复杂度远低于同类模型,为未来设计高性能多尺度动力系统模拟器提供了新的思路。
这是一项关于从数据中重构模型和发现物理规律的研究,该文章是复旦大学智能复杂体系实验室团队在AI for Science这一前沿领域的研究成果之一 [10,11]。复旦大学数学科学学院、智能复杂体系实验室博士生张静东为该论文第一作者,林伟教授、朱群喜博士为共同通讯作者。本研究得到了中国博士后科学基金、 上海市超级博士后计划以及上海市科学技术委员会、国家自然科学基金委、上海人工智能实验室、CFFF计算平台的支持。
论文连接:https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.L012031
Phys.org报道:https://phys.org/news/2024-02-machine-predictor-capability-intricate-physical.html
参考文献
[1] Zhang, J., Zhu, Q., & Lin, W. (2024). Learning Hamiltonian neural Koopman operator and simultaneously sustaining and discovering conservation laws. Physical Review Research, 6(1), L012031.
[2] Copernicus, N., Lerner, M. P., Segonds, A. P., Verdet, J. P., Luna, C., Savoie, D., & Toulmonde, M. (1965). De revolutionibus orbium coelestium (Vol. 1, pp. 4-4). Johnson Reprint Corporation.
[3]Kepler, J. (1997). The harmony of the world (Vol. 209). American Philosophical Society.
[4] Wang, H., Fu, T., Du, Y., Gao, W., Huang, K., Liu, Z., ... & Zitnik, M. (2023). Scientific discovery in the age of artificial intelligence. Nature, 620(7972), 47-60.
[5] Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378, 686-707.
[6] Greydanus, S., Dzamba, M., & Yosinski, J. (2019). Hamiltonian neural networks. Advances in neural information processing systems, 32.
[7] Liang, S., Huang, Z., & Zhang, H. (2021, October). Stiffness-aware neural network for learning Hamiltonian systems. In International Conference on Learning Representations.
[8] Fusco, G., Gronchi, G. F., & Negrini, P. (2011). Platonic polyhedra, topological constraints and periodic solutions of the classical N-body problem. Inventiones Mathematicae, 185(2), 283-332.
[9] Cai, S., Mao, Z., Wang, Z., Yin, M., & Karniadakis, G. E. (2021). Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mechanica Sinica, 37(12), 1727-1738.
[10] Zhang, J., Zhu, Q., & Lin, W.(2022). Neural Stochastic Control. In Advances in Neural Information Processing Systems.
[11] Zhang, J., Zhu, Q., Yang, W., & Lin, W. (2023). SYNC: Safety-aware neural control for stabilizing stochastic delay-differential equations. In The Eleventh International Conference on Learning Representations.











