因果关系的研究有着悠久的历史和重要的科学价值。自从300多年前乔治·贝克莱阐明“相关不意味着因果”以来,人们对因果关系展开了科学的探讨,建立了多种因果分析的理论框架和检测算法。其中,克莱夫·格兰杰创立的格兰杰因果关系检验方法因在经济学数据中的巨大应用而获得2003年诺贝尔奖;2021年的诺贝尔经济学奖也授予了在因果推断的方法学领域取得突出贡献的科学家。因果关系体现了各种自然现象和社会现象之间的内在必然联系,如何从观测时间序列数据中准确识别出变量之间的因果关系近年来受到了各领域学者的广泛关注,并在物理学、生态学、脑科学以及人工智能、精准医疗等多学科领域中取得了充分的应用。

然而,当前对于因果关系的科学定义存在多种不同的定量刻画,对应的检测方法也具有很多实质性完善的空间。于2022年5月4日发表于Research(Volume 2022,Article No. 9870149)的工作中,复旦大学数学学院、智能复杂体系基础理论与关键技术实验室林伟教授团队从因果关系的数学刻画——变量间的动力学迭代函数关系出发,基于分析学基础和动力学理论,提出了动力学因果框架——连续性标度,以动力学迭代函数本身的连续性来严格度量动力学因果关系。这一数学刻画化解了一直以来该领域的疑问:“为什么在动力学因果关系探测中‘用果投射因’,而在传统时间序列因果分析中‘用因评价果’?”。
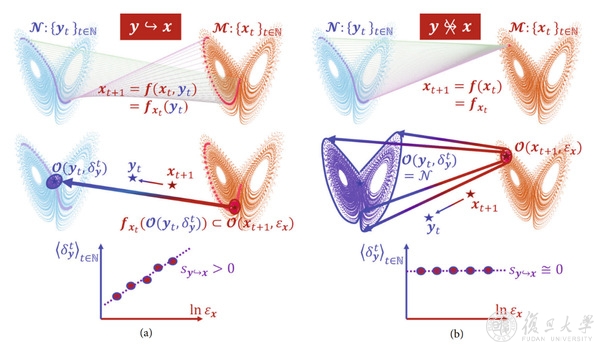
图1:动力学因果框架——连续性标度
同时,该团队还基于建立的数学刻画,给出了结合具体数据的因果探测与度量算法。相关算法在包括基因调控网络、海洋生态系统、新冠疫情传播机制、污染物与疾病互作系统等多个领域真实世界复杂系统的观测时间序列数据中得到了有效验证和充分应用,并且发现了一些符合第一性原理的新的因果连接。该动力学因果框架的建立,切实完善了动力学因果关系的理论和算法体系,为动态复杂系统核心结构辨识提供了有效途径,具有广泛的应用前景。
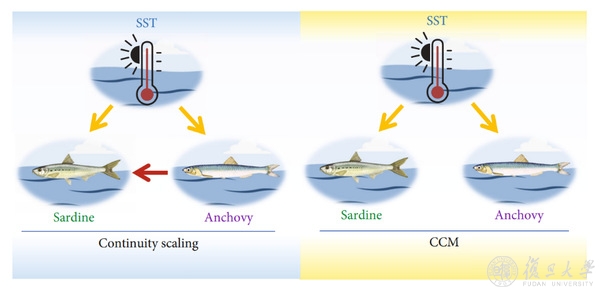
图2:连续性标度算法在海洋生态系统数据中的应用及对比
林伟教授及其团队多年来致力于应用数学和复杂系统理论与方法的发展,并促进智能科学、数据科学、生命科学、公共卫生等复杂系统领域实际问题的解决。复旦数学科学学院/智能复杂体系实验室博士生应雄、复旦工程与应用技术研究院青年研究员冷思阳为该论文共同第一作者。该研究得到了国家自然科学基金、教育部脑科学前沿中心、上海数学中心、上海人工智能实验室、上海市市级科技重大专项的资助和支持。
Research 文章链接:https://doi.org/10.34133/2022/9870149
