现实世界中的许多问题可以建模为动力系统,动力系统的平衡态蕴含了系统的主要信息,如何镇定具有不稳定平衡态的动力系统在控制领域中至关重要[1]。现实模型往往受到随机噪声和反应延迟的影响,因而需要对相应的动力系统引入随机项和时滞项进行建模[2]。但目前为止,对随机时滞动力系统安全镇定问题的理论研究和镇定器的算法设计还几乎是空白。
2023年1月15日,复旦大学智能复杂体系实验室林伟团队在International Conference of Learning Representation (ICLR)上发表了题为“SYNC: Safety-Aware Neural Control For Stabilizing Stochastic Delay-Differential Equation”的研究文章[3]。研究者提出随机时滞动力系统的稳定性和安全性理论,利用神经网络和障碍函数方法,在国际上率先构建出了具有稳定性和安全性保证的随机时滞动力系统镇定器,包括确定性镇定器和随机镇定器,以及建立了镇定器的能量损耗和镇定时间上界的理论估计,发现了随机控制优于确定性控制的反直觉现象,对理解并利用具体情境中噪声的作用具有重要意义。

一.利用LaSalle原理构建基于神经网络的确定性镇定器
研究者首先通过对描述随机时滞动力系统稳定性的LaSalle原理[4]的充分条件进行提取,得到了便于神经网络训练的损失函数,并利用正则化的方法构建参数化神经网络,得到了基于LaSalle原理的神经网络确定性镇定器(NDC),该镇定器可以方便地部署到自治或非自治随机时滞动力系统上。图1展示了NDC在Chua’s circuit的驱动-相应系统中的应用,与传统的基于全局李雅普诺夫函数的线性反馈镇定方法(LC)相比[5],NDC在自治(图1(c))和非自治(图1(d))情况下均具有更好的性能。LaSalle原理中的Ito微分算子使得耗散项在损失函数中以正定型的形式出现,导致该方法无法用于寻找随机镇定器,为此,研究者提出新的稳定性理论来寻找随机镇定器。
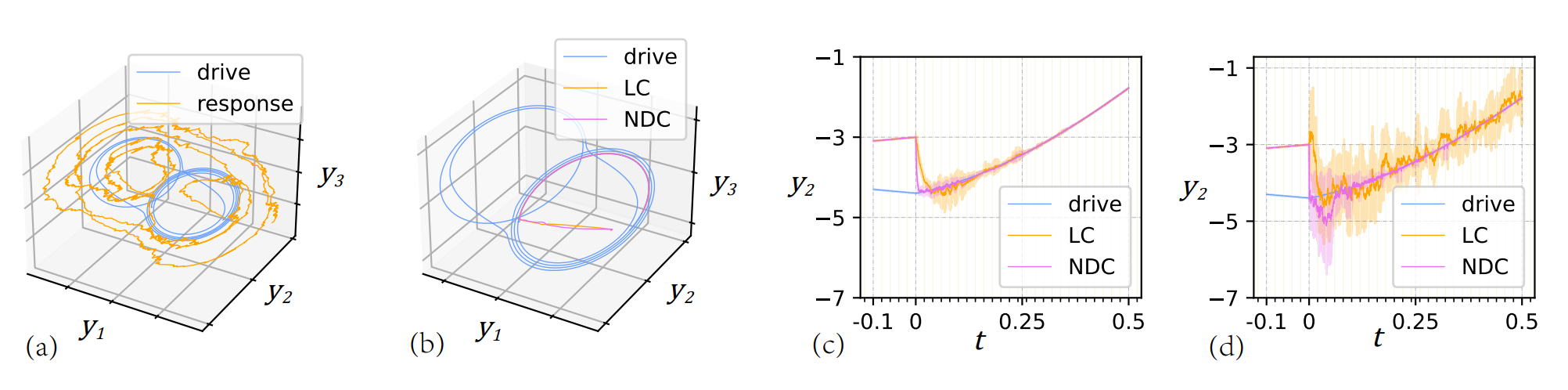
图1确定性镇定器在驱动-响应系统中的应用。
(图源:J Zhang, et al., ICLR, 2023)
二.构建基于神经网络的随机镇定器
研究者利用分数次状态变量的二阶微分性质,建立了条件简明的随机泛函系统(随机时滞系统为特殊的随机泛函系统)的稳定性理论,在此基础上构建了神经网络随机镇定器(NSC)。并且该方法不仅可以用来寻找随机镇定器,也可以寻找确定性镇定器。图2展示了所构造的镇定器在控制运动车辆抵达目标位置的结果,与基于在线学习的二次规划(QP)相比,NDC和NSC可以根据当前观测状态瞬时给出控制值,能更好地应用在实时控制任务中。与NDC相比,NSC控制下的轨道波动更大,但也会更快到达目标位置。

图2 随机镇定器和确定性镇定器在车辆运动控制中的应用。
(图源:J Zhang, et al., ICLR, 2023)
接下来,研究者计算分析了不同镇定器在车辆运动任务中的性能表现,其中,Tt为训练神经网络所需要的时间,E0.001为时间Tt之前的控制过程消耗的能量,Nd为受控轨道到目标位置的最短距离,E为受控轨道的模长首次达到0.001的时间。通过比较计算出的各项指标,研究者发现随机镇定器需要的时间和能耗最少,说明随机项并非是破坏系统稳定性的因素,而是在适当设计下有利于系统的稳定性。研究者进一步建立了随机镇定器和确定性镇定器的收敛时间和能耗的理论估计来验证这一发现。
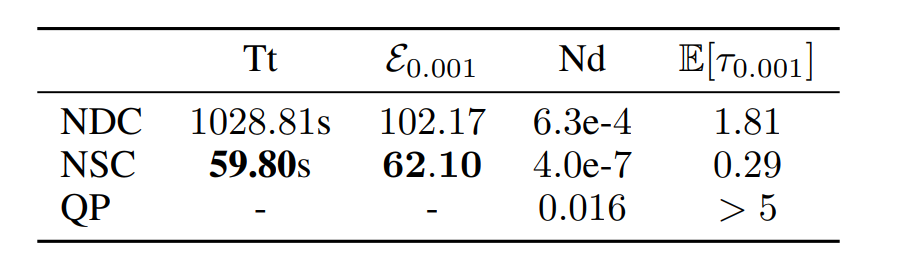
表1 车辆运动模型的控制结果。
(表源:J Zhang, et al., ICLR, 2023)
三.神经网络镇定器的安全性和稳定性保证
与确定性动力系统不同,随机动力系统的一个显著特征是稳定的动力系统的相空间轨道并不总是有界的,即无法保证系统轨道在指定安全区域内(图3左)。此外,由于计算机只能处理有限多数据,基于启发式学习的神经网络镇定器无法保证受控系统在全空间上满足稳定性条件。为解决这两个问题,研究者首先基于障碍函数理论[6]提出了随机时滞动力系统的安全性理论,得到概率1意义下的安全性。在安全性理论基础上,基于局部Lipschitz条件和有界区域上的有限剖分(图3右),研究者将安全区域进行有限网格离散化,构造了格点上的强安全性条件,使得强安全性条件在格点上满足时可以得到原安全性条件在整个安全区域上满足。用这些有限格点作为训练样本,强安全性条件作为损失函数,即可得到神经网络镇定器的安全性保证。在得到受控系统的安全性保证之后,系统解的存在空间即为安全区域,类似安全性保证的方式,在该区域上进行类似的离散化操作可以得到神经网络镇定器的稳定性保证。图4展示了安全性保证的神经网络随机镇定器在镇定不稳定倒立摆任务中的表现,与在线优化的方式(QP,MPC)和原始的随机镇定器相比,安全性保证的随机镇定器可以有效满足安全性约束。

图3 稳定随机系统不一定满足安全性约束(左)。离散化操作(右)。
(图源:J Zhang, et al.,ICLR, 2023)
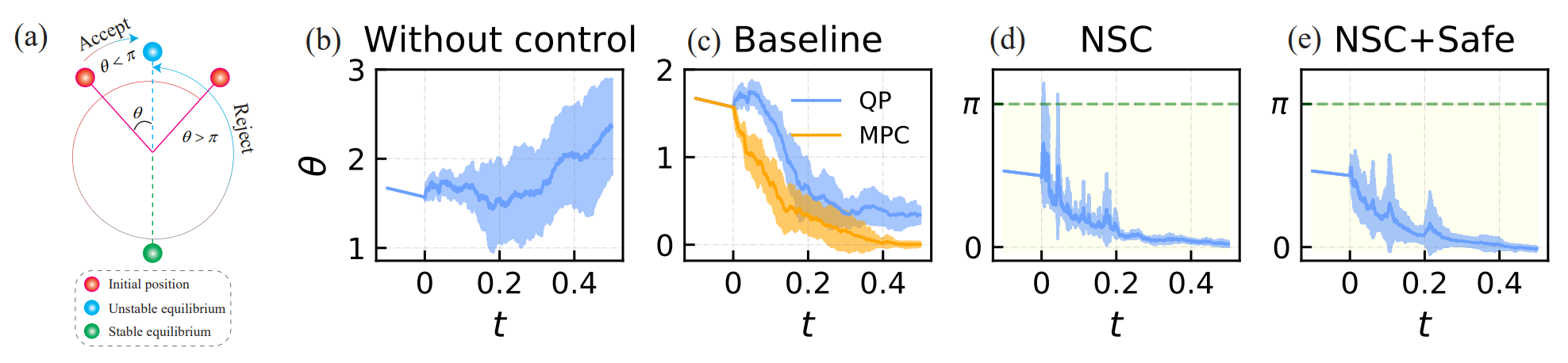
图4 安全性保证的随机镇定器在倒立摆模型中的表现
(图源:J Zhang, et al., ICLR, 2023)
文章结论与讨论,启发与展望
综上所述,该研究在国际上率先建立了利用随机控制来镇定随机时滞动力系统的稳定性和安全性理论,并建立了稳定性和安全性保证的神经网络镇定器算法。根据实验数据计算分析了确定性镇定器和随机镇定器在能耗和受控轨道收敛时间的表现,与确定性控制相比,随机控制具有更低的能耗和更快的收敛时间。该项研究为理解噪声在复杂系统中扮演的角色提供了新的视角,也可以通过适当的设计来利用噪声,而不是将噪声视为有害项来抑制。值得指出的是当前这项研究还有一些不足,比如,当前的研究主要是基于模型的研究,不能直接应用到基于数据的免模型情境中;且目前考虑的系统自由度较低,对高自由度系统的镇定控制,未来还需要更多的理论研究。
原文链接:
https://openreview.net/forum?id=_8mS2NE-HXN
这是一项关于神经网络控制器的研究,该文章是一系列研究成果之一[7]。复旦大学张静东博士生为该论文第一作者,复旦大学智能复杂体系实验室博士后朱群喜、杨伟高级工程师、林伟教授为共同通讯作者。本研究得到了中国博士后科学基金(2022M720817),上海市超级博士后(2021091),上海市科学技术委员会(22JC1402500, 22JC1401402,2021SHZDZX0103,21511100200,22ZR1407300),国家自然科学基金(11925103)的支持。
参考文献
[1] Wiener, N.(2019).Cybernetics Or Control And Communication In The Animal And The Machine. MIT Press. Cambridge.
[2]Xuerong Mao.(2007).Stochastic Differential Equations And Applications. Woodhead Publishing. Cambridge.
[3] Zhang, J., Zhu, Q., Yang, W., & Lin, W. (2023). SYNC: Safety-aware neural control for stabilizing stochastic delay-differential equations. In The Eleventh International Conference on Learning Representations.
[4] Xuerong Mao. Lasalle-type theorems for stochastic differential delay equations. Journal of mathematical analysis and applications, 236(2):3.
[5] Wei Lin and Yangbo He. Complete synchronization of the noise-perturbed chua’s circuits. Chaos:
An Interdisciplinary Journal of Nonlinear Science, 15(2):023705, 2005.
[6] Ames, A. D., Xu, X., Grizzle, J. W., & Tabuada, P. (2016). Control barrier function based quadratic programs for safety critical systems. IEEE Transactions on Automatic Control, 62(8), 3861-3876.
[7] Zhang, J., Zhu, Q., & Lin, W. Neural Stochastic Control. In Advances in Neural Information Processing Systems.
