2023年9月29日,《物理评论快报》(Physical Review Letters)在线发表了复旦大学林伟教授、秦伯韡副研究员团队的研究论文“Modulating Biological Rhythms: A Noncomputational Strategy Harnessing Nonlinearity and Decoupling Frequency and Amplitude”[1]。该工作中,研究人员揭示了解耦生物振荡频率和振幅的普适性理论,并在此基础上提出了易用高效的调频调幅控制器设计方法。

振荡在生命系统中普遍存在,例如,昼夜节律、神经元脉冲发放、心跳等。频率和振幅是生物振荡的重要表征,前者刻画了上游信号的特征,决定了下游功能是否启动,后者则调节了功能的强弱[2]。具有适当频率和振幅的振荡对保持生命系统健康运行至关重要。异常的频率或振幅会导致节律紊乱并进一步引发诸如睡眠障碍、二型糖尿病、抑郁症等各类生理或心理疾病[3,4]。此时,便需要利用系统自身的调频调幅机制或通过人工干预的方法将频率、振幅调节至正常水平。其中,如何实现单独调控频率或振幅而维持另一个量恒定不变长期以来受到来自生命科学及相关交叉领域研究人员的特别关注。数十年来,在这一方向上涌现了许多优秀的开创性工作。有学者揭示了频率可调性与生物振荡系统反馈回路模式之间的关联[5];也有学者利用数学模型列举了针对特定系统少数可行的调频调幅控制器[6],并被其他学者通过生物学实验得到验证[7];同期,也有研究者提出了生物振荡的线性反馈调控方法与理论[8,9]。这些工作虽然成功,但是有时候需要繁琐、复杂、消耗大量资源的大规模计算,或仅针对特定系统有效。这些限制在一定程度上给实际应用带来了挑战。因此,发展一种便于理解与使用的通用调频调幅原理和控制器设计方法变得非常有理论价值和现实意义。
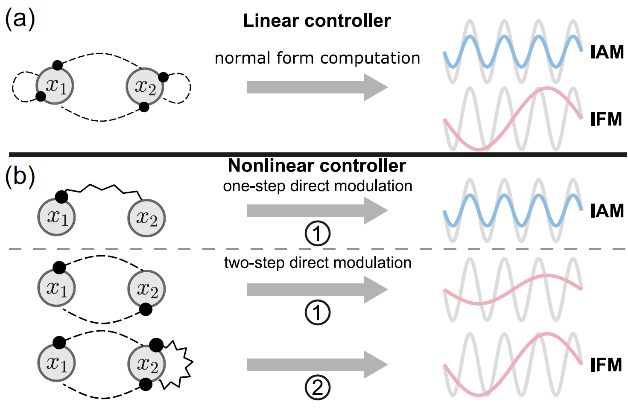
图 1 非线性控制器实现独立调幅与独立调频,避免了繁琐、复杂的计算。
为解决这一问题,复旦大学团队在最新的研究中基于普适的生物振荡动力学模型通过严格的数学理论构建了频率和振幅的精确定量刻画。然后,经过一系列理论及计算分析揭示了一个易用的频率振幅解耦原理。利用这一原理,研究人员可以巧妙地利用生物系统中普遍存在的非线性动力学,无需复杂繁琐的计算便能设计出可单独调节频率或振幅的反馈控制器(图1)。
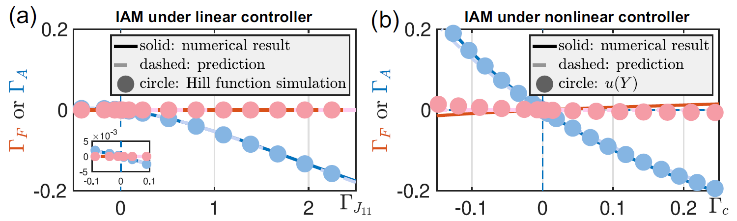
图 2非线性控制器以更小的代价实现更广范围的振幅调控。
为了验证有效性,研究人员将所提出的非线性反馈控制器应用于几类典型的生物振荡系统中。首先,作者将新方法与现有的线性反馈控制器在经典的遗传振荡器中进行了比较。新方法不仅规避了复杂的计算,也可以通过更小的代价实现更大范围的振幅调控(图2)。随后,在蛋白质-蛋白质交互系统中,非线性反馈控制器的有效性得到了进一步验证。通过调节其中一个蛋白质的动力学行为,可以同时实现所有蛋白质浓度的振幅调控(图3)。该现象也得到了相应数学理论的支撑。最后,作者也在复杂网络中对非线性控制器这一独特效果进行了展示。仅通过调节Watts-Strogatz小世界神经网络上单一节点的输入信号即可实现对所有节点振幅的调控。

这一研究工作不仅为生物振荡系统的调频调幅建立了相对完备的数理基础,频率、振幅解耦原理的揭示也为在不久的将来助力生物学家实现合成生命系统的调频调幅提供了原理指引。该工作是复旦团队在过去十年于“生物振荡调频调幅基础理论与关键算法”这一领域的系列成果之一[8,9]。复旦大学数学科学学院、智能复杂体系基础理论与关键技术实验室的博士生仲昭月为论文的第一作者,林伟教授、秦伯韡副研究员为共同通讯作者。本研究得到了科技创新2030—“脑科学与类脑研究”重大项目、国家自然科学基金、上海市科学技术委员会、上海市教育委员会和上海人工智能实验室的支持。
【参考文献】
[1]Z. Zhong, W. Lin, and B.-W. Qin, Modulating biological rhythms: A noncomputational strategy harnessing nonlinearity and decoupling frequency and amplitude, Phys. Rev. Lett.131, 138401 (2023).
[2]A.S. Hansen, and E.K. O’Shea, Limits on information transduction through amplitude and frequency regulation of transcription factor activity, eLife4, e06559 (2015).
[3]J. Bass, and J.S. Takahashi, Circadian integration of metabolism and energetics, Science330, 1349-1354 (2010).
[4]F. Rijo-Ferreira, and J.S. Takahashi, Genomics of circadian rhythms in health and disease, Genome Med.11, 82 (2019).
[5]T.Y.-C. Tsai, Y.S. Choi, W. Ma, J.R. Pomerening, C. Tang, and J.E. Ferrell, Robust, tunable biological oscillations from interlinked positive and negative feedback loops, Science321, 126-129 (2008).
[6]M. Tomazou, M. Barahona, K.M. Polizzi, and G.-B. Stan,Computational re-design of synthetic genetic oscillators for independent amplitude and frequency modulation. Cell Syst.6, 508-520.e5 (2018).
[7]F. Zhang, Y. Sun, Y. Zhang et al., Independent control of amplitude and period in a synthetic oscillator circuit with modified repressilator, Commun. Biol.5, 23 (2022).
[8]T. Ge, X. Tian, J. Kurths, J. Feng, and W. Lin, Achieving modulated oscillations by feedback control, Phys. Rev. E90, 022909 (2014).
[9]B.-W. Qin, L. Zhao, and W. Lin, A frequency-amplitude coordinator and its optimal energy consumption for biological oscillators, Nat. Commun.12, 5894 (2021).
原文链接:https://link.aps.org/doi/10.1103/PhysRevLett.131.138401
